
Frank van Hertrooij
Scivolemo 14 April 2018
Pliaj artikoloj
La 14an de marto, fanatikuloj de matematiko festas π-tagon. En la Usona sistemo por skribi datojn, la 14a de maro estas 03-14, kio korespondas al la unuaj decimaloj de la nombro π, nome 3,14. Multaj aliaj landoj skribas datojn malsame, sed tio ne signifas ke ili bezonas maltrafi π-tagon. La 22an de julio estas la ”alproksimiĝo de π”-tago pro tio ke la divido 22/7 estas ĉirkaŭ 3,14. Ironie, 22/7 estas pli preciza alproksimiĝo de π ol 3,14, do se oni nur enkalkulas la tagon kaj monaton, π-tago mem ne estas la plej bona alproksimiĝo, sed tio ne signifas ke oni rezignu de festi la gravan rolon kiun la nombro ludis en matematiko kaj scienco.
Historio de kalkuli π
Jam antaŭ pli ol 3000 jaroj, π estis konata en Babilonio kaj Barato. Tie, oni donis la valoron 3 al la nombro. Estis multaj antikvaj socioj, kiuj rimarkis ke la perimetro de cirklo ĉiam estas iomete pli ol trifoje la longo de la diametro de la sama cirklo. Kompreneble tiu scio estis tre utila por kiam oni laboras kun radoj. La problemo estis ke malgraŭ tio ke la difino de π estis tre simpla, la rilatumo inter la perimetro kaj diametro de cirklo, la nombro mem ne estis bela. Oni ne povas precize skribi π, sed anstataŭe povas senfine aldoni novajn decimalojn. Tio estis la komenco de konkurso, kiu daŭras ankoraŭ hodiaŭ, pri kiu povas kalkuli la plej precizan reprezenton de π. La antikvaj Egiptoj sukcesis kalkuli ke π estus 3,16 per kompari la perimetron de cirklo al tiu de regula oklatero (formo kun ok egalaj anguloj kaj flankoj). Neniu venkis tiun kalkulon ĝis Arĥimedo. Same kiel la Egiptoj, li alproksimiĝis al cirklo per plurlatero, sed lia formo uzis 96 laterojn. Ne estas malfacila vidi ke tiu formo multe pli similas al cirklo ol oklatero kaj tiel li eltrovis ke π proksimas al 22/7. La ideo malantaŭ la teĥniko estas ke oni povas desegni plurlateron kiel triangulon, kvadraton, aŭ oklateron en cirklo, tiel ke la anguloj tuŝas la cirklon. Oni povas vidi ke la perimetro de tiu formo estas iomete malpli granda ol tiu de la cirklo, sed la perimetro de plurlatero estas multe pli facile kalkulebla. Por esti eĉ pli precize, oni povas desegni plurlateron ĉirkaŭ la cirklo, tiel ke la cirklo tuŝas la mezpunktojn de la lateroj. Tiel la perimetro de la plurlatero estas iomete pli granda ol tiu de la cirklo, kio signifas ke la perimetro de la cirklo devas troviĝi inter tiuj de la du plurlateroj. Ju pli da flankoj la plurlateroj havas, despli preciza tiu alproksimiĝo iĝas kaj se oni kapablus desegni plurlateron kun senfine multe da lateroj, tiu havus ekzakte la saman perimetron kiel la cirklo kaj tion oni povas uzi por kalkuli la valoron de π.
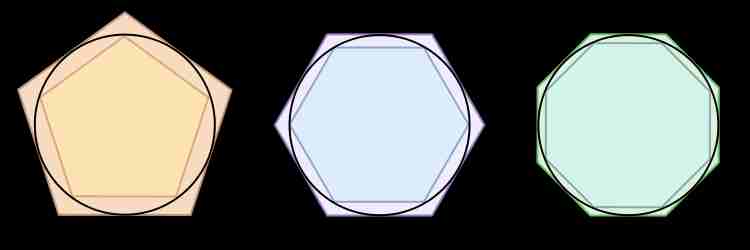
Sendepende de Eŭropo, ankaŭ la anktikvaj Ĉinoj serĉis alproksimiĝon de π. Zang Heng (張衡), kiu naskiĝis en la jaro 78 uzis la alproksimiĝon √10 (ĉ. 1,62) por kalkuli la volumon de sfero. Tio tre proksimis al la valoro kiun la Egiptoj eltrovis. En la jaro 263, Liu Hui (劉徽) verkis libron kun solvoj de problemoj el unu el la plej fruaj matematikaj verkoj el la Ĉina historio, “La naŭ ĉapitroj de matematika arto” (九章算術). En siaj komentoj pri la unua ĉapitro, li uzis plurlateron kun 192 lateroj por kalkuli π. Poste li faris eĉ pli precizan kalkulon per 3072 lateroj kaj esprimis la solvon kiel 355/113, kio estas ĉirkaŭ 3,1415929. Ĉi tiu valoro estis tiom preciza, ke dum jarcentoj neniu kapablas plibonigi ĝin.
La sekva revolucio okazis en Barato en la 14a jarcento, kie la matematikisto Madhava el Sangamagrama (സംഗമഗ്രാമ മാധവൻ) kalkulis la valoron de π ĝis 11 decimaloj, kvankam kelkaj homoj pensas ke li eĉ kalkulis 13 aŭ 17. Por atingi tiom grandan precizecon, Madhava ne uzis plurlaterojn kiel Arĥimedo aŭ Liu Hui, sed senfinan serion. Oni neniel povas esprimi π kiel la rezulton de algebraa ekvacio kun fina kvanto da faktoro. Tio signifas ke kalkuloj kiel 22/7 aŭ 355/113 nur povas esti alproksimiĝoj. Anstataŭe, Madhava eltrovis ke oni povas trovi la valoron de π tiom precize kiel oni volas per ekvacio kun senfine multe da faktoroj kaj termoj. Li komencis per 1 kaj subtrahis 1/3, poste adiciis 1/5 kaj denove subtrahis 1/7. Tion oni povas fari senfine longe, per pli kaj pli etaj nombroj. Depende de kiom da termoj oni uzas en la serio, la rezulto ŝanĝiĝas, sed kiom oni rigardas kie la rezultoj troviĝas sur la nombrolinio, oni vidas ke la rezulto estas pli proksima al π se oni uzas pli da nombroj.
Eŭropo estis malpli rapida kaj bezonis du jarcentojn pli por atingi la saman paŝon. Matematikistoj el diversaj landoj komencis krei senfinajn seriojn kaj produktojn por finfine igi siajn kalkulojn pli precizaj. La Franco François Viète publikigis ”Variorum de rebus mathematicis responsorum, liber VIII” en 1593, kiu enhavis senfinan produkton, kiu multfoje uzas √2. La ideo malantaŭ la metodo estas ke la rilatumo inter la surfaco de kvadrato kaj oklatero estas √2/2. Ellaborante tion por pli kaj pli da plurlateroj, oni povas alproksimiĝi al la rilatumo inter la surfaco de kvadrato kaj cirklo kaj uzi tiun por kalkuli π.
La Germana Nederlandano Ludolph van Ceulen tiom entuziasmis pri la nombro π ke li kalkulis ĝian valoron ĝis 35 decimaloj. Post lia morto en Nederlando, lia edzino eĉ skribis la nombron sur lia tombŝtono. Iom malpli preciza versio de 32 decimaloj troveblas en lia libro “Vanden circkel”, kiun li publikigis en 1596. Lia peno estis honorigita per monumento en 2000 kaj en kelkaj Eŭropaj landoj, specife en malnova literaturo, la nombro π estis nomata la nombro de Ludolf.
Eble la plej impona alproksimiĝo finiĝis en 1873 de la Brita amatora matematikisto William Shanks. Dum dudek jaroj li kalkulis novajn decimalojn dum la matenoj kaj kontrolis ilin posttagmeze. Finfine li sukcesis kalkuli 707 decimalojn, kvankam oni poste eltrovis ke nur la unuaj 527 estis ĝustaj. La atingo estas tamen tre speciala, pro tio ke li ne havis komputilon kaj pro tio ke oni nur bezonas ĉirkaŭ 60 decimalojn por kalkuli la perimetron de la observebla universo kun precizeco de unu longo de Planck. Tio signifas ke Shanks kalkulis π multe pli precize ol oni iam ajn bezonus por fizika problemo.
Kiam oni ekuzis komputilojn, oni pli kaj pli rapide trovis novajn decimalojn de π. La nura afero kiu estis bezonata por trovi pli da decimaloj estis bona senfina serio, rapida komputilo kaj multe da tempo kaj pro tio, kalkuli la decimalojn estis ofte uzata por montri kiom bona nova komputilo estis, dum la komputiloj iĝis pli kaj pli fortaj. Krom tio, pli da decimaloj ne havas veran utilon, sen oni daŭre kalkulas novajn decimalojn por plibonigi la rekordon.
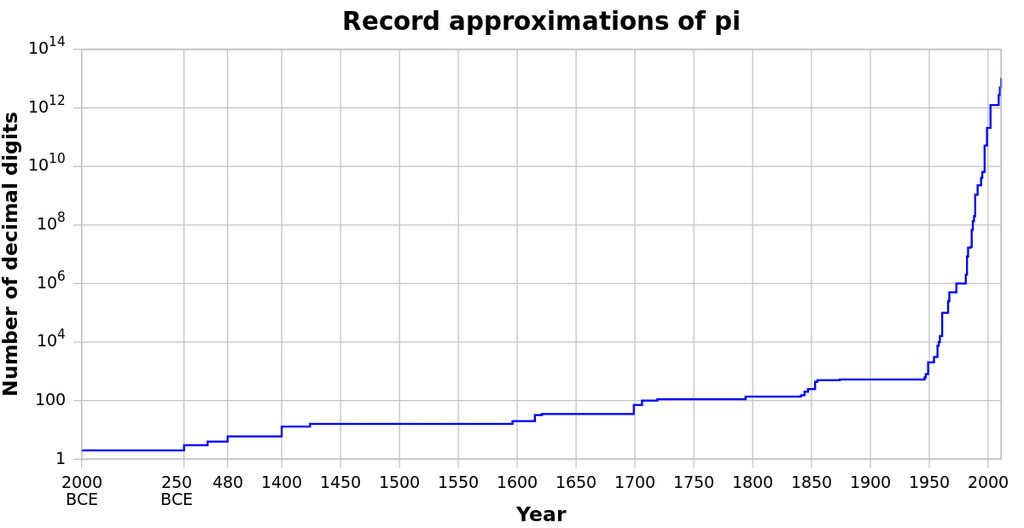
Uzoj de π en fiziko
La nombro π estas tre utila kaj troviĝas en multaj problemoj kaj ekvacioj. Ĝi eĉ havas rolon en la unua ekvacio en la historio de fiziko, kiu priskribas pendolojn. Preskaŭ ĉiam, kiam oni vidas π, la problemo iel rilatas al cirkloj. Tio signifas ke geometriaj problemoj tre ofte uzas π, sed ankaŭ aliaj kampoj de matematiko kaj scienco estus nenie sen ĝi. En fiziko oni uzas π en meĥanikaj problemoj, kiuj priskribas rotaciojn. Por priskribi forton, kiu tiras objekton en cirklon, ekzemple la forton per kiu globoĵetisto tenas la globon, oni uzas la formulon 1, en kiu F estas la forto, m estas la maso, r estas la distanco inter la globo kaj la centro de la cirklo kaj T estas la daŭro de unu rondiro. Tiu sama π aperas en aliaj ekvacioj, kiel la tria leĝo de Kepler, kiu priskribas la rilatumo inter la distanco inter planedo kaj tiel stelo kaj la tempo kiun ĝi bezonas por rondiri. Ĝi aperas tie, pro tio ke la fortoj inter la stelo kaj la planedo funkcias same kiel tiu inter la globo kaj la ĵetisto.
1:
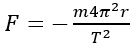
Alia loko kie oni renkontas π estas en la leĝo de Coulomb, kiu priskribas kiom granda la forto inter du elektraj ŝarĝoj estas. Ĝi estas tre grava en kvantummeĥaniko por priskribi kiel elektronoj agas. La ekvacio por tiu leĝo estas formulo 2, en kiu F estas denove la forto, q1 kaj q2 estas la ŝarĝoj de partikloj, e0 estas konstanto kaj e estas la distanco inter la partikloj. Kvankam la ekvacio ne aspektas kvazaŭ ĝi rilatas al cirkloj, la π ne estas tie por nenio. La elektra forto disvastiĝas en ĉiuj direktoj, kio signifas ke la kampo havas la formon de sfero. Oni povas priskribi la surfacon de tiu sfero per 4πr2 kaj tio gvidis al la formulo. La ekvacio kiu priskribis la gravitan forton ankaŭ povus esti verkita tiumaniere, sed anstataŭe π estas kaŝita en la gravita konstanto, do ĝi ne estas videbla. Kiel konsekvenco tamen, ĝi reaperas en aliaj formuloj.
2:
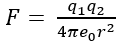
En ĉi tiuj formuloj, sed ankaŭ multaj aliaj, π ne venas sole, sed estas obligita de 2 aŭ kvar 4. La kaŭzo de tio estas ke oni difinis π per la diametro de cirklo, la distanco inter du ekstremaj punktoj de cirklo. Ĉio alia en fiziko kaj matematiko estas skribita per la radiuso tamen, kiu estas nur la distanco de ajna punkto de la cirklo al la centro. La diametro estas do dufoje tiom longa kiel la radiuso. Interesa alternativo estas τ (prononcata kiel ”taŭ”). Tiu nombro estas definita kiel la rilatumo inter la perimetro kaj radiuso de cirklo. Pro tio, ĝi estas dufoje tiom granda kiel π, do oni ne bezonas aldonan faktoron de 2 se oni kalkulas per τ. Malfacilas ŝanĝi kutimon kiu ekzistas jam dum pluraj miljaroj, do por la videbla estonteco, π restos la plej uzata cirklokonstanto.
Interesaĵoj pri la decimaloj de π
La nombro π havas kvalitojn, kiuj ne ĉiuj nombroj havas. Pro tio, ĝi estas membro de kelkaj interesaj kategorioj. Unue, π estas neracionala nombro. Tio signifas ke oni ne povas kalkuli ĝin per dividi du entjeroj (… -2, -1, 0, 1…). Dividoj kiel 22/7 estas bonaj alproksimiĝoj, sed oni neniel povas ekzakte priskribi π tiel. Neracionalaj nombrojn havas senfine multajn decimalojn sen paterno. Ĉi tiun kvaliton ankaŭ aliaj konataj nombroj havas, kiel √2. Fakte ekzistas senfine multe da neracionalaj nombroj. Ne estas multaj homoj tamen, kiuj emas parkerigi ĉiujn decimalojn de √2.
Malkiel √2, oni eĉ ne povas skribi π kiel la radiko de polinomo kiu konsistas el racionalaj koeficientoj. Tio igas π transcenda nombro. Ankaŭ transcendaj nombroj estas tre oftaj, sed pro tio ke pruvi transcendeco estas tiom malfacila, oni ne konas multajn malsamajn ekzemplojn.
Aldone, ekzistas multaj indikoj ke π estas normala nombro. Tio signifas ke neniu sinsekvo de decimaloj estas preferata kompare al alia. La nombro trapasas ĉiujn statistikajn testojn por kontroli tion, sed pruvi ke ĝi vere estas normala nombro ne estas tiom simpla. Ke neniu sinsekvo estas preferata signifas ke π estas unu el la plej bonaj metodoj por akiri hazardajn nombrojn kiu ekzistas. Fakte, se oni konas sufiĉe da decimaloj de π, oni povus retrovi ajnan sinsekvon de nombroj. Se oni do transskribus la Fundamenton de Esperanto al cifera kodo, oni povus retrovi ĝin en π aŭ alia normala nombro.
Neniu nombro havas tiom grandan rolon en populara kulturo kiel π, do malgraŭ tio ke ĝi havas multajn mankojn, ĉiu povas konsenti pri tio ke π havas gravan historion. La tago de π do ne nur ekzistas por festi la ekziston de π, sed ankaŭ por pripensi la homojn kiuj penis dum jaroj por malkovri pli da decimaloj kaj la sciencistoj kiuj uzis la nombron por ŝanĝi la mondon.