
Frank van Hertrooij
Scivolemo 09 Novembro 2021
Pliaj artikoloj
Mi konas magian trukon, kiu tiel facilas ke ĉiu povas fari ĝin. Simple prenu kartaron kaj miksu ĝin, ĝis ĝi estas tute hazarda. Nun rigardu la sinsekvon de la kartoj. Nenio speciala, ĉu? Male! Ĉi tiu sinsekvo estas tiel speciala, ke neniu homo vidis ĝin antaŭe. Eble mia truko ne povas imponi vin, sed ĝi utilas en alia maniero. Ĝi povas instrui al ni ion pri kiel varmo kaj energio funkcias, kiel oni konstruu maŝinojn, kaj eĉ ion pri la sekretoj de la universo. Antaŭ tio, indas iom trankviliĝi kaj rigardi la kartojn denove. Kiel mi fakte povas esti tiel certa pri la unikeco de ilia sinsekvo?
Ĉiu kartaro estas unika
Kiam oni volas kalkuli probablecojn, oni ofte volas scii en kiom da manieroj io povas okazi. Ĉi-kaze la demando estas kiom da sinsekvoj ekzistas por konata nombro de kartoj. Se la nombro de kartoj estas malalta, oni povas simple serĉi tiujn sinsekvojn permane. Jen ekzemplo kun tri kartoj:
A B C
A C B
B A C
B C A
C A B
C B A
Oni povas provi sisteme trovi ĉiujn sinsekvojn. Sed se la nombro de kartoj iĝas eĉ iomete pli granda, oni ne plu sukcesos. La nombro de sinsekvoj simple eksplodos. Oni povas ordigi 4 kartojn en 24 manieroj, 5 kartojn en 120 manieroj, 6 kartojn en 720 manieroj kaj tiel plu.
Pli simpla maniero por kalkuli tiujn rezultojn estas per multiplikado. Simple imagu ke vi havas tri kartojn en la mano, kiujn vi volas meti en tri lokojn sur la tablo. Oni povas kalkuli la nombron de eblaj sinsekvoj per multipliki la nombroj de malplenaj spacoj por ĉiu karto. Oni konsideru tamen ke tiu nombro ŝanĝiĝas ĉiun paŝon. La unua karto havas tri malplenajn spacojn, dum la dua karto havas nur du. La tria karto eĉ ne havas elekton, ĉar restas nur unu spaco. Tio signifas ke la fina nombro de sinsekvoj estas kalkulebla per simpla multiplikado de 3∙2∙1. Notu ke ĉi tiu strategio facile ĝeneraligeblas. Se oni volas scii la nombron de sinsekvoj de 6 kartoj, oni multiplikas 6∙5∙4∙3∙2∙1 kaj trovas 720 kiel rezulton. Pigraj matematikistoj kaj sciencistoj uzas la simbolon ! por tio. Anstataŭ skribi 6∙5∙4∙3∙2∙1=720, ili simple skribas 6!=720 kaj diras ”Ses faktoriale estas sepcent dudek.”

Multaj poŝkalkuliloj havas specialan butonon por faktorialoj, por ke oni ne bezonu tajpi longajn listojn de ciferoj. En la kazo de kartludo, tiu butono ne multe utilos tamen. La valoro de 52!, la nombro de eblaj sinsekvoj de tuta kartludo, simple tro grandas por kutima poŝkalkulilo. Bonŝance aliaj homoj kalkulis ĉi tion antaŭe kaj metis la rezulton en la interreto. Ĝi estas ĉirkaŭ 8∙1067. Se oni skribus tiun nombron plene, ĝi havus 68 ciferojn. Ne estas surprizo ke oni uzas krisignon por tiaj numeroj. Ili povas esti timigaj! Fakte, konsideru ke aĝo de la universo ekde la praeksplodo estas ĉirkaŭ 4∙1017 sekundoj. Tio estas nombro kun 18 ciferoj. En aliaj vortoj, se oni unike miksis okilionon da kartaroj ĉiun sekundon ekde la praeksplodo, oni malkovris nur unu elcenton de la eblaj sinsekvoj. Estas klare ke se oni vere miksas hazarde, ĉiu sinsekvo kiun oni vidos dum homa vivo estos unika.
Matematika petanko
Unu el la plej interesaj uzoj de faktorialoj estas nombri kombinaĵojn. Tio signifas ke oni kalkulas en kiom da manieroj oni povas preni ion el kolekto de objektoj. Se oni ŝatas kartludojn, oni ekzemple povas interesiĝi pri kiom da malsamaj kombinoj de kvin kartoj oni povas preni el kartaro. Tion oni kalkulas per la ekvacio 52!/(5!∙47!) = 2598960. Mi ne tro detale priskribos kiel ekzakte oni trovas tiajn formulojn, sed unu punkto estas grava: Oni faras nenion pli malsimplan ol multiplikado kaj dividado!
Se oni igas la formulojn eĉ pli kompleksaj, oni povas solvi pli interesajn problemojn, kiuj pli similas al la naturo. Ni povas formeti la kartaron nun, sed necesas ankoraŭ unu plisimpligita modelo por plene kompreni kiel la universo funkcias. Eble oni nomu ĝin la ”Petanko-Modelo” (Petanko estas franca ludo kun metalaj globoj). Imagu ke oni estas petankludisto kaj havas du belajn skatolojn por transporti la globojn, kiel en la bildo sube. La sola diferenco estas ke oni estas tiel granda amanto de petanko, ke oni havas 1000 globojn. Aldone, 100 el la globoj estas iomete pli specialaj. Ili estas orkoloraj anstataŭ ŝtalkoloraj.

Se oni tute hazarde plenigas la skatolon, oni ne povas antaŭvidi ĉu la oraj globoj estos ĉefe en la dekstra, aŭ la maldekstra skatolo. Oni povas atendi ke ambaŭ skatoloj enhavos 50 orajn globojn, sed ankaŭ 48 en unu kaj 52 en la alia estus tute ebla. Se oni kunmetas la formulon kiu priskribas ĉi tiun situacion, oni povas kalkuli ke ekzistas 5∙10138 malsamaj aranĝoj en kiuj ambaŭ skatoloj enhavas ekzakte 50 orajn globojn. Tio ne diras multe, sed oni povas uzi la saman formulon ankaŭ por aliaj distribuoj de oraj globoj. La grafeo sube montras kiel tio aspektas por ĉiuj eblaj aranĝoj de 0 oraj globoj en la dekstra skatolo ĝis 100 oraj globoj en la dekstra skatolo.
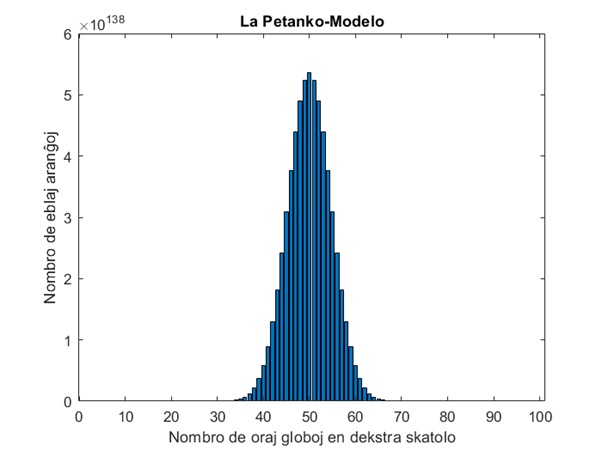
La distribuo klare montras ke la nombro de eblaj aranĝoj por nombro de oraj globoj inter 43 kaj 57 sufiĉe altas, sed rapide malkreskas ekster tiuj limoj. 70 orajn globojn oni esence neniam trovus en unu skatolo. Ĉi tiu kompreno estas nekredeble forta. Oni tute hazarde plenigas la skatolojn, do je mikroskopa nivelo ĉiu aranĝo same verŝajnas. Malgraŭ tio, oni klare vidas diferencojn je la makroskopa nivelo. Fizikistoj nomas tiun efikon entropion. Ĝi estas mezuro de kiom verŝajna stato de sistemo estas surbaze de la nombro de eblaj aranĝoj. Oni povus diri ke la stato en kiu ambaŭ skatoloj enhavas 50 orajn globojn havas altan entropion, dum la stato kun ĉiuj oraj globoj en la dekstra skatolo havas tre malaltan entropion.
La statistikoj de teo
Unu el la plej bongustaj entropiaj eksperimentoj kiujn oni povas fari estas la preparado de teo. La solaj paŝoj kiujn oni bezonas fari estas varmigi la teon kaj enmeti la saketon. Oni povas kompari ĉi tiun eksperimenton al la Petanko-Modelo, ĉar ĝi estas bazita sur hazardaj aranĝoj: la molekuloj de la teo estas puŝataj en hazardaj direktoj de la akvomolekuloj; ili estas tiom malgrandaj ke ili apenaŭ influiĝas de gravito; kaj se oni zorge enmetas la saketon, la akvo ne tro multe fluas en la taso.

Se oni rigardas la tason atente, oni vidas kiel la teo fluas el la saketo kaj malrapide difuziĝas en la akvo. Estas kvazaŭ iu nevidebla forto dispuŝas la temolekulojn. Sed tia forto ne ekzistas, almenaŭ ne en la kutima senco de la vorto. La difuziĝo vere estas simpla statistika efiko. La filmeto sube estas tre simpla modelo de teo, kiu sekvas nur tri regulojn:
1. En la komenco, ĉiuj temolekuloj troviĝas en la saketo
2. En ĉiu tempopaŝo, ĉiu partiklo povas movi unu paŝon horizontale aŭ vertikale
3. La partiklo elektas sian direkton tute hazarde. Nur se ĝi trafas muron, ĝi restas
Mi aldonis neniujn regulojn pri la sekvado de gradientoj aŭ ion similan. La molekuloj moviĝas tute hazarde, sed tamen havas klarajn tendencojn je la makroskopa nivelo. La klarigo de tiu kompleksa konduto denove estas entropio. En la komenco, ĉiuj temolekuloj estis en la tesaketo. Estas relative malmultaj aranĝoj de la molekuloj, kiuj plenigas tiun kondiĉon, do la teo havis malaltan entropion. Poste, la teo komencis movi al proksimaj aranĝoj kaj eskapis la saketon. Estas klare ke stato en kiu la teo plenigas grandan volumenon havas pli da eblaj aranĝoj, ĉar la molekuloj simple havas pli da eblaj pozicioj. Je la fino, la teo estis egale distribuita en la taso kaj havis la plej grandan nombron de aranĝoj. Tio estas la stato kun la plej alta entropio. Ĝenerale oni vidas ke ordigita sistemo (ĉiu partiklo en la saketo) grade iĝas homogenaj.
La modelo montras ke se eblas, entropio kreskas. Se la entropio de la sistemo estas relative malalta, ĝi spontanee iras al stato kun pli alta entropio. Tiu observo estas la dua leĝo de termodinamiko. Ĝi priskribas la difuziĝon de molekuloj, sed ankaŭ la fluon de varmo, la direkton de ĥemiaj reagoj kaj eĉ la efikecon de datenkunpremo! Interesa eco de la leĝo estas ke ĝi iĝas des pli vera, ju pli da partikloj la sistemo havas. Mia modelo enhavas 160650 partiklojn de teo, sed la kvantoj de partikloj kiujn oni uzas en ĥemiaj eksperimentoj estas pli proksimaj al 1023: nombro kun 24 ciferoj.
Vivaĵoj kiel entropiaj fabrikoj
Kiam oni kalkulas la entropion de malsamaj statoj de molekulo, oni pensu pri multaj aferoj. Ne nur temas pri kiel libere molekuloj moviĝas en la solvaĵo, sed ankaŭ pri kiel facile ili rotacias, vibras kaj ĝenerale ŝanĝiĝas. Tio multe dependas de la strukturo de la molekulo. Ĉenforma molekulo multe pli libere ŝanĝas sian formon ol ringformaj molekuloj. Tio havas gravajn konsekvencojn por vivantaj organismoj, ĉar ili konsistas el multaj grandaj, kompleksaj molekuloj. Kiel tio eblas?
Kutima tipo de reagoj en biologiaj organismoj estas polimerigado. Tio estas reago per kiu la korpo kreas grandajn ĉenformajn molekulojn kiel proteinojn aŭ DNAn el malgrandaj unuoj: la monomeroj. Unuavide, oni povas pensi ke tiaj reagoj rompas la duan leĝon de termodinamiko. Polimero havas malpli altan entropion ol liberaj monomeroj, ĉar la libereco de moviĝo de la monomeroj estas limigita. Por tamen plenigi la kondiĉojn de la dua leĝo de termodinamiko, iu alia parto de la sistemo devas kompensi. Bestoj faras tion per manĝado. Por ĉiu molekulo de glukozo (baza unuo de sukero kaj amelo), la korpo povas liberigi ses molekulojn da akvo, ses molekulojn da karbondioksido kaj iom da energio. En tiu procezo la entropio tiel multe kreskas ke la korpo povas uzi ĝin por malpliigi sian propran entropion. Tio signifas ke malgraŭ tio ke biologia organismo havas tre malaltan entropion, ĝi konvertas manĝaĵojn al produktoj kun pli alta entropion kvazaŭ iu entropia fabriko. Tio pluiras ĝis la organismo mortas kaj ankaŭ ĝi atingos termodinamikan ekvilibron.
Oni ne bezonas tiel kompleksajn sistemojn por vidi ĉi tiun efikon parenteze. Oni povas observi ĝin en la propra kuirejo. Se oni plenigas bovlon per akvo kaj enmetas kelkajn gutojn de oleo, oni vidas ke la oleo ne difuziĝas. Ĝi formas vezikojn je la surfaco. Por kompreni tion, oni pripensu ke la oleo ne estas la sola substanco en la sistemo. Ankaŭ la akvo kontribuas al la entropio. Se akvomolekulo troviĝas inter siaj amikoj, ĝi facile turniĝas. Ĝi interagas same facile kun ĉiuj molekuloj. Je la surfaco de olea molekulo, la situacio estas malsama. Akvo ne facile interagas kun oleo, do ĝi havas preferatajn turniĝojn, for de la oleo. Ke la libereco de turniĝado estas limigita signifas ke la nombro de aranĝoj por la akvomolekuloj estas limigita, do la entropio estas malalta. Se la oleaj molekuloj tuŝas unu la alian, io interesa okazas. La surfaco inter la akvo kaj la oleo iĝas malpli granda, do la kvanto de akvomolekuloj kun limigita turniĝado malkreskas. Tio pligrandigas la nombron de aranĝoj de la akvomolekuloj kaj plialtigas la entropion. La areo estas minimumigata kaj ronda veziko kreiĝas. La entropio de la oleo certe malaltiĝis, sed la entropio de la akvo tiel multe altiĝis, ke ĝi povas kompensi.

La strukturo de la kosmo
Iom pli grandskala temo estas la formiĝo de strukturo en la kosmo. Nuboj de gaso aŭ polvo kolektiĝas en kreskantaj steloj kaj planedoj, iĝante pli kaj pli kompleksaj. Oni povas demandi sin kial tio ne rompas la duan leĝon de termodinamiko, sed la antaŭaj ekzemploj provizas solvon: se la entropio de parto de la sistemo malkreskas, alia parto devas kompensi. Ekzemploj de tio estas abundaj kaj troviĝas eĉ en la Sunsistemo.
Jupitero estas la plej granda planedo en la Sunsistemo kaj konsistas ĉefe el gaso. Pro ĝia grandeco, ĝi ankaŭ havas fortan gravitan kampon, per kiu ĝi tiras la gason al la kerno. Dum ĝia tuta ekzisto ĝi faris tion, sed ĝi ankoraŭ ne atingis ekvilibron. La diametro de la planedo daŭre malkreskas. Tio sonorigu la alarmon, ĉar gaso en malpli granda volumeno havas malpli da eblaj aranĝoj. Ĝia entropio malkreskas! Alia observo kiun oni povas fari estas ke la gaso gajnas kinetikan energion. Same kiel pilko kiu falas de turo, ĝi akcelas pro la gravita tiro. Tiu aldona energio esprimiĝas kiel plialtiĝo de la temperaturo de la gaso. La plivarmiĝo de gasoj kiuj rapide kunpremiĝas estas universala. Ĝi okazas ankaŭ se oni rapide kunpremas gason per piŝto aŭ alia maŝino. Ankaŭ la malo veras. Se oni uzas fajroestingilon kun kunpremita CO2, la fino de ĝia tubo iĝas tiom malvarma ke glaciaj kristaloj formiĝas sur ĝi. Eble tiu rilato inter volumeno kaj temperaturo gvidas al la fonto de la ekstra entropio.

La maniero per kiu astronomoj observas la temperaturon de la interno de Jupitero estas sufiĉe interesa. Ĝi estas bazita sur la fakto ke ĉio kun temperaturo brilas. Tio videblas kiam la temperaturo estas sufiĉe alta. Se oni varmigas najlon, ĝi unue iĝas ruĝa kaj poste pli kaj pli blanka, depende de ĝia temperaturo. Ankaŭ la koloro de stelo dependas ĉefe de la temperaturo de ĝia surfaco. Oni povas kalkuli ke ankaŭ objektoj kun malpli altaj temperaturoj devas brili, sed la ondolongo de tiu radiado estas tro longa por esti detektata de homaj okuloj. Multaj bestoj kaj artefaritaj detektiloj vidas la mondon tute malsame. Per infraruĝa kamerao oni povas detekti la lumon produktata de homoj kaj eĉ vidi la temperaturajn diferencojn inter malsamaj korpopartoj. Tiun koncepton oni uzis ankaŭ por observi Jupiteron. Oni vidis ke Jupitero elsendas pli da energio en la formo de (nevidebla) lumo ol ĝi ricevas de la Suno. Se oni subtrahas ĉiujn aliajn fontojn de energio, eblas konkludi ke la varmo vere estas rezulto de kunpremado de gaso.
Ŝajne Jupitero ne rompas la duan leĝon de termodinamiko. Ĝi perdas entropion pro ĝia malkreskanta volumeno, sed la pli alta rapido de la partikloj kaj la fakto ke ili povas ĉiam elsendi lumon, aŭ ne, faras ke la tuta nombro de eblaj aranĝoj nur kreskas.
Nigraj truoj
Se oni kunpremas gason ekstreme multe, io speciala okazas. Ekstreme pezaj steloj je la fino de sia vivo simple kolapsas. La internaj fortoj ne plu kapablas rezisti kontraŭ la gravito kaj la stelo iĝas pli kaj pli eta, ĝis ĝi atingas esence senfinan densecon. La gravita forto proksime al tia objekto estas tiom forta ke nenio plu povas eskapi. La stelo iĝis nigra truo. Ĝi nomiĝas tiel pro la ideo ke eĉ lumo ne povas eskapi ĝin. Tio ne estas malĝusta ideo, sed nigraj truoj tamen ne estas tute nigraj. Ili ja produktas iomete da lumo per nenio alia ol entropio.
Oni povas rigardi nigran truon kiel unudirektan membranon. Objektoj povas eniri, sed ne eliri. El termodinamika perspektivo tio estas problemo, ĉar la nigra truo cenzuras la objektojn kiujn ĝi konsumas kaj esence forviŝas ilin el la universo. Devas esti iu maniero en kiu la entropio de la objekto estas konservata tamen, ĉar tion postulas la dua leĝo de termodinamiko.
Grandan kontribuon al la termodinamika priskribo de nigraj truoj faris Jacob Bekenstein. Li malkovris ke la areo de la eventa horizonto de nigra truo similas al entropio en multaj manieroj. Tiu eventa horizonto estas la limo de la nigra truo. Ĝi estas regiono en la spaco preter kiu oni ne povas eskapi. La ekzakta diametro de tiu regiono dependas de la maso de la nigra truo, ĉar pezaj nigraj truoj havas pli fortan gravitan kampon. Oni povas konkludi do ke la areo de la eventa horizonto devas kreski se la nigra truo konsumas mason. Se oni faras la kalkulojn, oni eĉ povas ĝeneraligi la duan leĝon de termodinamiko. La sumo de la entropio kaj la areo de ĉiuj nigraj truoj en la sistemo restas konstanta, eĉ se la nigraj truoj konsumas unu la alian. Tiu intima rilato inter la areo de la eventa horizonto kaj entropio faris ke iliaj priskriboj interplektiĝis. La areo de la eventa horizonto estas ĝia entropio.
Estas klare ke nigraj truoj havas entropion, sed tio havas konsekvencojn. Specife se oni konsideras la trian leĝon de termodinamiko. Tiu diras ke la entropio de objekto kun temperaturo de 0K (ĉirkaŭ -273⁰C), la absoluta minimumo de la universo, estas nula. Inverse, ĉio kio havas entropion devas havi temperaturon. Tio ligas la laboron de Jacob Bekenstein al tiu de Steven Hawking, kiu esploris meĥanismon per kiu nigraj truoj povus liberigi partiklojn. Tiu Hawkingradiado estas kompleksa interago inter kvantummeĥaniko kaj relativeco. Ĝi estas bazita sur la fakto ke, eĉ en vakuo, tuttempe kreiĝas tielnomataj virtualaj partikloj. Ili kreiĝas en paroj el kiuj unu havas pozitivan kaj unu negativan energion. Post mallonga tempo ili renkontiĝas kaj malaperas denove, tiel ke la totala energio restas konstanta. Ĉu tio fakte okazas dependas de perspektivo tamen. Se oni ne akcelas kompare al la partikloj, ili restas virtualaj, sed se estas akcelo, ili povas iĝi veraj. Tio signifas ke oni vidas nenion se oni falas en la nigran truon, sed vidas verajn partiklojn se oni restas je fiksa distanco. Tiumaniere, pozitiva energio povas eskapi kaj la maso de la nigra truo malkreskas. La lumo kiu eskapas havas la spektron kiun oni atendas de varma objekto kaj la entropio kiun ĝi kontribuas al la universo kompensas tiun de la objektoj kiujn la nigra truo konsumis. La dua kaj tria leĝo de termodinamiko restas konsistaj eĉ en la plej ekstremaj situacioj.

Ĉu nigraj truoj nigras aŭ ne? Tio dependas de ilia temperaturo. Grandaj nigraj truoj havas malaltan temperaturon kaj elsendas nur malmulte da Hawkingradiado. Ili fakte absorbas pli da radiado ol ili elsendas. Nur en fora estonteco, kiam la universo estos eĉ pli disstreĉita ol ĝi estas hodiaŭ, la nigra truo estos pli varma ol sia medio kaj komencos malkreski. Nigraj truoj kies maso estas ĉirkaŭ 60% de tiu de la Luno jam pli varmas ol la medio kaj multe radiumas. Ju pli malgranda ili estas, des pli hele ili brilas. Tre malgranda nigra truo eĉ povus havi videblan koloron. Malgraŭ tio, sciencistoj ankoraŭ ne konfirmis ajnan observon de Hawkingradiado el nigra truo. Eble estas eraro en la teoria priskribo, aŭ eble ne ekzistas nigraj truoj kiuj estas sufiĉe helaj kaj proksimaj por observado. Tio estas defio por la novaj generacioj de astronomoj.
Danko
Mi ŝatus danki la matematikiston kaj Esperantiston Yann Chiffaudel, sen kies helpo mi ne povus fari la kalkulojn necesajn por ĉi tiu afiŝo.
Plua legado
Se vi volas scii pli pri nigraj truoj, entropio kaj la kosmo, rekomendinda libro estas “Mallonga historio de la tempo” (A brief history of time) de Steven Hawking. Ĝi parte inspiris min al verki ĉi tiun artikolon kaj ĝenerale estas tre interesa libro. Laŭ mia scio bedaŭrinde ne ekzistas Esperanta traduko, sed la libro estis tiel populara ke ĝi tradukiĝis al multaj naciaj lingvoj.